 开放以来,计算机与网络技术不断发展,大量的软件设计法应运而生,面向对象程序设计方法便是近年来在有限元程序设计等众多领域都有重要应用的方法,因此,全面系统地掌握面向对象方法学的含义与基本原则,有利于充分挖掘该方法的优势,从而为优化有限元程序设计提供有效助力。应用面向对象方法学时应建立适应现代人思维方式的描述范式,也就是说利用思维方式的问题模型设计相关软件,尽可能确保求解方法的自然性与准确性。一般情况下,面向对象方法包含概念对象、消息、类、继承、方法等关键元素,其中概念对象与消息的作用是描述两种事物之间的相互关联,类和继承表示描述范式,而方法则是各种操作行为。以面向对象方法学为基础的程序软件具有继承性、封装性及多态性的特点,能更加准确的感知各类对象之间的细微差别,是完善有限元程序设计的关键。另外,面向对象方法学为构建应用程序框架奠定了基础,有利于简化设计流程,设计人员需要提高重视程度,加快面向对象方法学分析与研究脚步。
开放以来,计算机与网络技术不断发展,大量的软件设计法应运而生,面向对象程序设计方法便是近年来在有限元程序设计等众多领域都有重要应用的方法,因此,全面系统地掌握面向对象方法学的含义与基本原则,有利于充分挖掘该方法的优势,从而为优化有限元程序设计提供有效助力。应用面向对象方法学时应建立适应现代人思维方式的描述范式,也就是说利用思维方式的问题模型设计相关软件,尽可能确保求解方法的自然性与准确性。一般情况下,面向对象方法包含概念对象、消息、类、继承、方法等关键元素,其中概念对象与消息的作用是描述两种事物之间的相互关联,类和继承表示描述范式,而方法则是各种操作行为。以面向对象方法学为基础的程序软件具有继承性、封装性及多态性的特点,能更加准确的感知各类对象之间的细微差别,是完善有限元程序设计的关键。另外,面向对象方法学为构建应用程序框架奠定了基础,有利于简化设计流程,设计人员需要提高重视程度,加快面向对象方法学分析与研究脚步。
1.2研究面向对象非线性有限元程序的意义
上世纪九十年代,学者们就已经提出了有限元思想,使人们认识到了有限元法的特点与优势。借助于计算机的应用与推广,有限元法在多种力学与材料分析中都有良好应用。与其他数值分析方法相比,有限元法在工程分析中更加灵活具体,近似程度也大幅度提升,利用该方法编写数值计算程序已经成为程序设计發展的必然趋势。传统程序一般由不计其数的代码构成,应用复杂的计算机语言进行组合编写,不仅晦涩难懂,还无法快速适应新方法、新模型带来的变化。
研究面向对象非线性有限元程序弥补了传统程序的不足,其研究意义主要体现在以下几个方面。其一是解决了代码重复利用的困难,在原有程序系统中,各部分数据结构紧密相连,与每个程序具有的独立功能原则相悖,容易导致各数据结构与功能相互依赖,无法重复利用一些代码,增加了设计人员的工作量。其二是避免细小变动影响程序的整体稳定性,全局可访问是数据结构的重要特征,如要改变某一部分代码则需要将相关代码全部改写,否则数据结构的功能将会发生变动。面向对象与非线性有限元理论解除了数据之间的依赖,最大程度地减少了设计任务量,能够促进有限元程序设计向着更好的方向发展。
2面向对象有限元基础设计与有限元基础类
2.1数值计算设计
完善的有限元程序应包含一个完整的线性代数库,建立该数据库需要运用矩阵类、矢量类、张量类等数值计算方法。1)矩阵类。与原有程序设计不同,有限元分析中不仅需要进行普通的实矩阵运算,还要进行稀疏矩阵运算,这类矩阵形式规模较大,增加了运算难度。为了解决这一问题,可以用继承树的形式进行计算,将组成矩阵的基本元素看做私有成员变量,运用矩阵赋值、相加、相乘、求逆、转置等方法进行求解。2)矢量类。矢量类的数值计算设计与矩阵类基本相似,但矢量在实际应用中具有特殊作用,不可一味地将矢量作为特殊的矩阵进行计算。矢量类虽然不存在继承树,但该种数值计算方法仍能保证涉及矢量计算的各类代码可以适度扩展。3)张量类。封装张量类一般不单独使用,原因是该种方法只能确定三维坐标系中的自身价值,不具有矩阵类与矢量类的优点。但张量类的数值计算设计保障了数据结构的完整性与系统性,有助于实现有限元程序的扩展和重用,可将其与其他数值计算方法进行深度融合,从而提升有限元程序设计水平。
2.2有限元模型设计
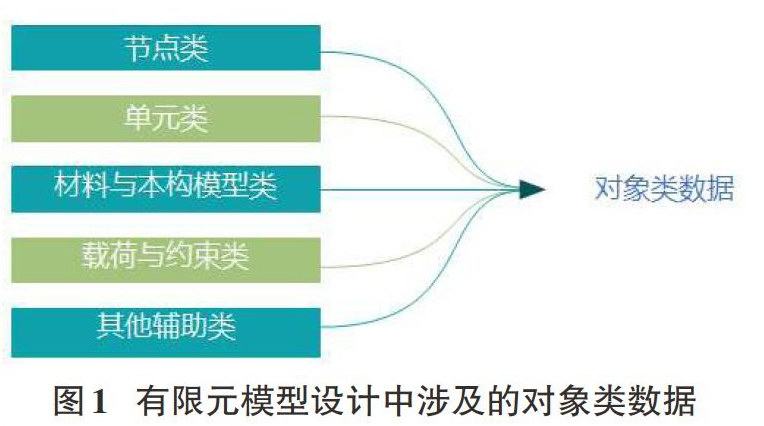
建立健全有限元模型需要对问题求解区域进行有限元离散,应综合考虑各方因素,协调各类能够单独封装成对象类的数据,为有限元模型的建立奠定基础。图一中所列的五种对象类数据是影响模型设计的关键因素,下文进行了详细论述。首先是节点类。运用程序进行工程分析时会涉及与节点有关的数据,为了确保分析的科学性与合理性,需要建立类来描述相关数据。类包括节点坐标、属性、节点力计算与分配等信息,在有限元分析中主要作为与其他类之间的通信提供接口。其次是单元类。单元主要表示有限元程序系统的拓扑属性,而单元类则是用来管理基础属性数据或计算单元荷载向量。简而言之,单元类能够完整封装数据,保证了单元的多态性。值得注意的是,单元类设计是有限元程序设计中的核心内容,需要仔细确认单元类包含的对象,计算单元自身对求解问题贡献的量,并注意求解结束后的一系列操作。再次是材料类。材料数据能够确定分析问题的性质,具有独立性特点,建立材料类对有限元模型有着重要影响。最后是载荷与约束类。节点荷载与单元荷载(包括约束条件)是有限元模型中的两类荷载,荷载类可以在规定时间内利用载荷时间函数求出每个部分的值。另外,荷载时间函数类、时间积分方案类与时间步骤等能够辅助完成模型设计中涉及的计算任务。
2.3有限元基础类库设计
类库在计算机程序设计应用中有着悠久历史,然而在面向对象有限元程序设计领域还缺少一个科学有效的类库,无法使有限元程序设计系统化。有限元基础类以微软基础类为基础,整合完善了有限元程序设计中需要的所有基本数据类,是建立在相对成熟系统的函数之上的C++类库。有限元基础类库能够显著提升设计效率,利用面向对象方法减少了代码的修改与重复。设计有限元基础类库需要保证具有良好的兼容性,原因是现代多数计算机的操作系统是Windows,要想设计的程序流程运行就必须与微软基础类(MFC)相互兼容。建立类库时还应进行有限元数据对象类整合,协调各部分数据之间的关系,从而提升数据结构之间的凝聚性。设计非线性有限元程序时应从实际问题出发,以分析研究非线性问题为主,尽量为用户预留最大接口,使其可以根据自身需要进行一定修改。有限元基础类库的优势是能够自动嵌入整体程序,不用设计人员再进行任何修改,提高了设计人员的工作效率。有限元基础类库还有利于构建应用程序框架,为设计人员提供了完整的设计思路。
2.4数据管理
有限元程序设计中运用了大量的数据,如何科学管理这些数据已经成为设计人员应重点思考的问题。为了方便用户使用,设计人员应从程序本身角度进行考量,使这些数据以更加直观的方式表达出来,提高界面的交互性。在面向对象有限元程序设计中,图形化界面的交互性良好,能够进行实时监控,提高了数据管理的效率与质量。有限元分析中包含的数据较多,模型类只能处理与自身相关的数据,需要运用求解域类管理相关数据。在求解域类中,储存了列表数据(单元、节点、材料、荷载、时间函数等),能够处理方程求解对象、读取与识别数据文件,具有非常重要的作用。求解域的首要任务是作为用户接口触发求解过程,并进行有效的模型部件管理,实现各部件之间的通信。举例来说,节点类、单元类的部件与数据文件之间的通信就是利用求解域实现的。除此之外,求解域还可以传达计算结果信息。
3面向对象非线性有限元分析算法
3.1非线性有限元分析理论
准确来说,结构力学属于非线性问题,运用线性假设无法有效解决结构力学难题。非线性问题主要分为三大类,需要根据实际情况进行界定,由于影响因素较多,在一定程度上增加了非线性问题分析的难度。下文以材料非线性问题和几何非线性问题为例介绍了非线性有限元分析理论。材料非线性问题需要将关注点放在本构关系上,将其在一个载荷步内线性化处理,同时注意相关参数设置的合理性与科学性,确保其满足非线性本构关系。有限元分析主要以材料的弹塑性为主,将荷载分解为多个增量,然后分别进行求解,将每部分增量用方程线性化,从而提高求解简便性。对于几何非线性问题,表达格式更加复杂,随着深入研究,非线性连续介质力学原理更加完善,运用该原理得出了解决几何非线性问题的一般格式,已经取得了良好的应用效果。Lagrange格式是研究得出的处理几何非线性问题的最有效格式,另外,还需要具体问题具体分析,进行一定的扩展设计。
3.2非线性有限元方程增量求解算法
从非线性有限元分析理论中可以得知,运用增量求解算法能够顺利计算非线性方程。增量求解算法在实际运用中需要遵循相关原则,以免破坏有限元方程计算结果的科学性与准确性。一般情况下,增量求解算法主要分为三类,分别是无迭代、变刚度迭代和常刚度迭代的增量求解方法,这三种方法具有各自的特点与使用范围。无迭代增量求解法的计算效率较低,主要适用于荷载增量小的情况,而且计算步骤复杂,每一个增量步骤都需要重新分析刚度矩阵,一定程度上影响了计算精度。常刚度迭代增量求解法不具有此缺点,只需分析处理首次形成的刚度矩阵即可,简化了求解步骤,从而降低了求解成本,有利于提升非线性有限元程序的经济效益与社会效益。正如硬币具有两面性,迭代增量求解法也存在缺陷,主要表现为收敛速度缓慢,且荷载越大速度越慢,不利于提升程序运行速度。设计人员应加大研究力度,解决求解质量与效率之间的矛盾,进而促进非线性有限元程序设计的健康发展。
4从应用程序框架角度分析非线性有限元程序设计
4.1应用程序框架
通过分析算法与有限元基础类的分析讨论可以建立一个应用程序框架。应用程序框架指的是具有强大凝聚性与组织性的类库,在该框架中可以实现消息数据的实时交流,還可以应用相关函数完成计算任务。构建应用程序框架需要以有限元基础类库为基础,赋予类库中封装好的类实用意义,利用具体的对象完成操作行为。设计人员应明确单元类、材料类、节点类等各大类之间的关系,进而构建整个应用程序框架的最外层结构。在静态情况下,有限元基础类库的对象类无法组建一个能够相互传递消息、调用对方函数的网络,需要将其与应用程序框架相结合才能完成面向对象非线性有限元程序的运行任务。设计人员需要营造集成开发环境,以此为设计工作提供简便高效的工具。营造集成开发环境的意义在于能够为工作人员提供使用的设计模板,通过在该模板上添加、删减代码,达到自己想要的效果。
4.2非线性有限元程序设计步骤
应用面向对象法与非线性有限元理论进行程序设计更加科学高效,设计人员只需利用简单的单元类进行两级结构设计就可形成一个完整的非线性有限元程序,极大地提高了设计人员的工作效率与质量。第一级设计是单元级设计,工作人员首先要掌握单元刚度的定义与利用单元类构建单元刚度矩阵的方法。如果单元级设计中不涉及非线性几何问题,可将其归为线性问题处理,反之则需要进行单独处理。第二级设计是总体级设计,通过非线性求解器的应用在每一个迭代步和增量步中求解相关问题。
4.3非线性有限元程序的扩展
从应用程序框架角度分析面向对象非线性有限元程序较为简单,只需在某一环节和接口中插入相关代码就可完成,也就是说通过已有对象类的继承和扩展使程序设计符合要求。首先是单元类的继承与扩展,有限单元分析中的单元类不具有可执行性,必须使用具体的单元,充分发挥面向对象的继承性和封装性。其次是材料类的继承与扩展,材料数据类与单元数据类相同,也需要依靠具体的数据进行运算设计。例如,可将材料数据基类分为具体的弹性材料类和塑性材料类,了解每一种材料类的属性与特点。最后是求解器类的继承与扩展,在求解非线性问题时,设计人员的任务是在线性化系统类的帮助下利用变刚度迭代和常刚度迭代方法解决问题。
5总结
综上所述,面向对象方法学与非线性有限元分析理论在有限元程序设计中有着至关重要的影响,设计人员应熟练掌握方法理论基础,从而利用有限元基础类库减少传统程序中存在的大量复杂数据结构。在今后的设计工作中,设计人员还应加强前后处理数据的管理,积极寻找更加有效的管理方式,提高有限元程序的可扩充性。另外,还应从程序框架角度优化有限元程序设计效果,从而使面向对象非线性有限元程序更加灵活地应用于工程分析,提高分析水平。
相关热词搜索: 程序设计 面向对象 有限元 方法 研究